Le point d’étoile fonctionne un peu comme un point à trois relèvements avec des amers, sauf que dans ce cas précis les relèvements sont remplacés par des droites de hauteur faites sur des étoiles. Pour que le point d’étoile soit précis il faut si possible utiliser des étoiles les plus éloignées possibles les unes des autres (dans l’idéal avec 120 degrés entre chaque étoile), et effectuer la mesure au sextant peu avant ou après le coucher du soleil pour pouvoir bien distinguer encore la ligne d’horizon. Il faut également éviter de choisir des étoiles trop proches de l’horizon à cause de la réfraction de la lumière (voir loi de Snell-Descartes). C’est difficile lors de l’emploi du sextant de »faire descendre l’étoile sur l’horizon » (on peut facilement confondre une étoile avec une autre à côté), c’est pourquoi il est plus simple de l’utiliser à l’envers (limbe vers le haut), c’est à dire de « faire monter l’horizon sur l’étoile » de son choix. Généralement on ne peut utiliser des étoiles que placées proche du point d’horizon où se couche le soleil, au-delà c’est chaud de bien distinguer de façon nette la ligne d’horizon pour avoir un angle précis.
Pour mettre en place ce petit programme j’ai utilisé en grande partie un mémoire de master en astrométrie (introduction aux coordonnées célestes, astrométrie, Jleborgne) provenant de l’université de Toulouse, trouvable facilement en pdf sur le net, et d’autres trucs glanés ici ou là.
1) Système de coordonnées, définitions, mouvements impliqués
a) Coordonnées célestes
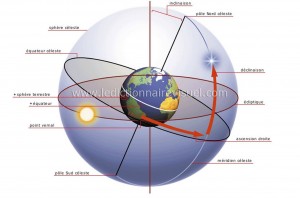
Le système utilise des coordonnées équatoriales; on va situer les astres selon leur position par rapport à l’équateur céleste qui n’est rien d’autre que la projection de l’équateur sur la sphère céleste. En fait c’est presque le même principe que pour se situer sur terre; pour positionner une étoile on va avoir:
–L’ascension droite souvent symbolisée par la lettre alpha, angle mesuré sur l’équateur céleste entre le point Vernal et la perpendiculaire à l’équateur céleste passant par l’objet étudié. Le point d’origine est donc le point Vernal et l’angle se mesure vers l’Est, cet angle s’exprime le plus souvent en heures mais est facilement convertible en degrés (1 heure=15 degrés, 1 degré=60 minutes, 1 minute=60 secondes), en heure elle varie donc de 0 à 24 heures (soit 0 à 360 degrés).
– La déclinaison souvent symbolisée par la lettre delta, angle mesuré perpendiculairement entre l’objet étudié et l’équateur céleste. Sa valeur peut monter au max à 90 degrés (-90 au pole sud et 90 au pole nord)et au minimum à 0 degrés (équateur). La déclinaison ressemble beaucoup à la latitude, elle est positive dans l’hémisphère Nord et négative dans l’hémisphère Sud.
–Le point Vernal souvent représenté par gamma ou simplement la lettre g, est un peu plus subtil à se représenter. Sur la sphère céleste l’écliptique (plan comprenant la terre et le soleil) et l’équateur céleste se croisent en deux endroits appelés noeuds, le noeud descendant quand le soleil passe de l’hémisphère Nord au Sud, et le noeud ascendant quand il passe de l’hémisphère Sud au Nord, bref à l’équinoxe de printemps (entre le 19 et le 21 mars).Nous allons voir que ce point de référence n’est pas fixe. En effet les équinoxes se déplacent d’environ 50 » par an le long de l’écliptique vers l’ouest. L’angle horaire du point vernal (ou temps sidéral) se compte à partir du méridien de Greenwich et on l’écrit généralement ahso ou ahgγ. Le point vernal se déplace presque selon une vitesse constante, cette vitesse fait environ 15.04166 degrés. Nous verrons que pour fiabiliser notre programme il va falloir encore plus de précision.
Pour les coordonnées célestes les coordonnées J2000.0 servent de référence, soit les mesures prises le 1er janvier 2000 à midi pile dans le calendrier Grégorien. Si on tape le nom d’une étoile dans wikipédia par exemple, la plupart du temps les coordonnées indiquées à droite de la page sont celles mesurées à J2000.0, pour avoir les bonnes coordonnées selon le moment de la mesure, des corrections à appliquer à ces valeurs sont indispensables.
b) Le calendrier Julien, calendrier Grégorien
Importants à comprendre pour faire notre programme; le calendrier Grégorien est un peu une version customisée du calendrier Julien, l’origine est la même tout comme les divisions en mois et semaines. La différence sera dans le choix des années bissextiles. Pour le calendrier Julien, il y a simplement une année bissextile tout les 4 ans (2008, 2012, 2016…) et pour le calendrier Grégorien, plus précis il y a une année bissextile si d’autres conditions supplémentaires sont réunies. Dans notre cas les caractéristiques du calendrier Julien suffiront. Bref dans le calendrier il y a 12 mois remplis alternativement par 31 (janvier, mars, mai, juillet, août, octobre, décembre) ou 30 jours (avril, juin, septembre, novembre). Exception pour février avec 28 jours pour une année « normale » et 29 jours pour une année bissextile, on arrive donc à 365 jours pour une année classique et 366 jours pour une année bissextile, soit une moyenne annuelle de 365.25 jours avec le calendrier Julien. Cependant cette durée ne colle pas parfaitement avec la durée réelle d’une année…Donc il va falloir bricoler un peu tout ce merdier pour que ça marche à peu prêt ! Un vrai boulot d’horloger stakhanoviste un peu maniaque sur les bords….
c) Qu’entend-t-on par « année » ?
Une année dans le calendrier Julien fait 365.25 jours. Mais il existe d’autres façons de qualifier une année:
–Année sidérale : révolution terrestre rapportée à un repère fixe. Elle dure environ 365 jours, 6 heures, 9 minutes et 10 secondes.
–Année tropique : temps entre deux passages successifs du soleil dans la direction du point vernal. Cette durée va être primordiale pour notre programme, notamment dans le calcul de l’angle horaire du point vernal. Elle dure environ 365 jours, 5 heures, 48 minutes et 45.26 secondes à J2000.0. Pour notre siècle elle décroit d’environ 5.23 secondes.Il y a une formule pour calculer l’année tropique moyenne trouvable un peu partout sur le net, c’est :
Année tropico =365.24219052-61.56*10^(-6)*T-0.068*10^(-6)*T^2+263*10*(-9)*T^3+3.2*10^(-9)*T^4. En 2000 elle vaut 365.2421898 jours et en 2100 elle vaut 365.2421291582 jours. T est le temps écoulé en siècles Juliens depuis J2000.0.
–Année anomalistique : temps entre deux passages successifs de la terre au périhélie. Elle dure à peu prêt 365 jours, 6 heures, 13 minutes et 53 secondes. Le périhélie c’est le moment où la Terre est la plus proche du Soleil (lois de Kepler), donc là où elle se déplace le plus vite.
d) Mouvements influant sur les coordonnées équatoriales
Pour notre plus grand malheur ces coordonnées ne sont pas stables (se serait trop simple), elles vont évoluer selon deux phénomènes cycliques appelés la précession et la nutation. La précession est due aux effets de marée sur la rotation de la terre. C’est un mouvement lent d’une période de 26000 ans environ mais de très grande amplitude car il peut monter jusqu’à 23.5 degrés environ (modifier la déclinaison d’un astre jusqu’à 23.5 degrés). La nutation due également à la marée a une période brève de 18.6 ans avec une amplitude faible comparativement à la précession : 9 secondes seulement. Du coup pour notre programmation, et aussi pour simplifier tout ça on peut négliger la nutation, on y perd un peu en précision mais bon…
On va utiliser ces formules pour le programme :
–Précession générale=p=50.290966+0.0222226T » par an, T temps écoulé en siècles Juliens (36525 jours) depuis J2000.0.
-p=m*cos(E)+n*sin(E), E inclinaison moyenne de l’écliptique (23°26’21.448 » à J2000.0). m est la précession en ascension droite, n est la précession en déclinaison.
-p=5029.0966+2.22226T-0.000042T^2 » par siècle.
-m=4612.4362+2.79312T-0.000278T^2 » par siècle.
-n=2004.3109-0.85330T-0.000217T^2 » par siècle.
La précession donne à la Terre une sorte de mouvement de « balle liftée » par rapport au soleil. Elle provoque également un changement d’étoile polaire; actuellement c’est Polaris qui indique le Nord mais ce ne sera pas éternellement le cas.
d) autres phénomènes impliquant des corrections
On va y trouver la réfraction atmosphérique bien sûr (loi Snell-Descartes), mais également l’aberration de Bradley, la parallaxe, la hauteur de l’observateur par rapport au niveau de la mer, l’erreur de demi-diamètre de l’astre observé. L’erreur de demi-diamètre de l’astre (voir droite de hauteur) est négligeable car une étoile c’est petit vu de notre position; on peut également ignorer la parallaxe en raison de l’éloignement important des étoiles, donc de sa valeur infime ici. On peut aussi s’en tamponner de l’aberration de Bradley…Heureusement on va quand même tenir compte du reste histoire que ça fonctionne un minimum !
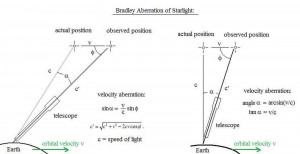
Aberration de Bradley : ce phénomène existe à cause de la vitesse finie de la lumière (environ 300000 km/s dans le vide) et de la rotation de la terre autour du Soleil (environ 30 km/s, varie selon sa trajectoire elliptique). Cela provoque en une année une légère rotation de toutes les étoiles autour de leur « point moyen » sur la voûte céleste; en fait l’étoile n’est pas fixe mais tourne autour d’un tout petit cercle ou une ellipse. La différence entre la position moyenne et apparente de l’étoile est de 20.5 secondes… Ce qui est relativement peu donc pour le programme on peut s’en balancer.
Cette différence entre position moyenne et apparente s’explique avec la formule présente dans le schéma ci-dessus : tan(alpha)=v/c ; or sur terre v=30 km/s environ et c=300000 km/s. Donc tan(alpha)=0.0001, donc alpha=0.00573°=20.6265 ».
Anecdotes :
.c’est difficile de se représenter ce phénomène mentalement, et comme on dit « un schéma synthétique vaut toujours bien mieux qu’un long discours un peu chiant », une analogie de situation peut-être bien pratique. Il y a l’analogie de Bradley lui même grâce à sa pratique de la voile sur la Tamise en observant un drapeau : ce dernier n’est ni dans le sens du vent, ni dans le sens de direction du bateau mais dans la composante vectorielle des 2. C’est pareil pour la position de l’étoile résultant de la composante vitesse de la Terre autour du Soleil avec la vitesse de la lumière.
. La parallaxe est utilisée comme outil pour savoir approximativement les distances d’éloignement de certains astres. Pour les étoiles les plus proches du système solaire la valeur de la parallaxe ne dépasse pas 1 seconde d’arc…Du coup on va pas trop s’embêter avec ça hein.
La correction de la réfraction atmosphérique varie selon la pression atmosphérique et la température ; sur wikipédia on nous donne une formule à employer quand on est au niveau de la mer, à pression atmosphérique constante de 1010 mbars avec une température de 10 °C. Cette formule, semblable d’ailleurs à celle du mémoire (c’est la même mais simplifiée) est la suivante :
R=(1.02/tan(Hv+10.3/(Hv+5.11)))/60 ; R est l’angle de réfraction en degrés, Hv est la hauteur vraie en mètres.
La dépression apparente de l’horizon, due à la hauteur de l’observation par rapport au niveau de la mer est trouvable sur plusieurs pages du web avec la formule suivante :
D=(1.77*√(E))/60 , D abaissement de l’horizon en degrés et E élévation de l’oeil en mètres.
e) Comment mesurer la hauteur d’une étoile ?
C’est le même principe que la droite de hauteur avec le Soleil. C’est l’angle horaire du point vernal qu’il faut utiliser, il va nous permettre de déterminer l’angle horaire local ahl de l’étoile :
ahl = ahgy – g + AV (g est la longitude du point estimé e, AV est l’ascension verse).
L’ascension verse est l’angle entre le méridien du point vernal et celui d’un astre mesuré comme un angle horaire, vers l’ouest et sur 360 degrés; elle est utilisée en nav astro pour situer une étoile.
L’ascension droite est l’angle entre le méridien du point vernal et celui d’un astre, mesuré vers l’Est et exprimé en heures. C’est le complément à 360 degrés de l’ascension verse. Par exemple l’ascension verse en janvier 2016 pour Bételgeuse est de 270.985 degrés. Donc l’ascension droite sera égale à 360-270.985=89.015 degrés. En général quand on cherche la position d’une étoile sur le net elle est donnée en déclinaison et ascension droite, à J2000.0.
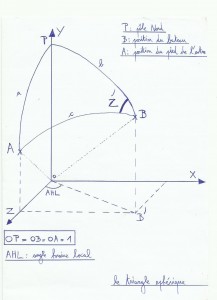 Comme pour la droite de hauteur avec le soleil (voir droite de hauteur), les formules à intégrer pour les calculs sont les suivantes :
Comme pour la droite de hauteur avec le soleil (voir droite de hauteur), les formules à intégrer pour les calculs sont les suivantes :
-sin (hc) = sin (L) * sin (D) + cos (L) * cos (D) * cos (AHL) ; hc est la hauteur calculée de l’astre, L la latitude du point estimé e, D la déclinaison de l’astre, et AHL c’est l’angle horaire local.
-cos (z^) = (sin (D) – sin (L) * sin (hc)) / (cos (L) * cos (hc)).
– Le relèvement calculé de l’astre est égal à z^ si 180°≤AHL<360°, et à 360-z^ si 0≤AHL<180°.
-L’intercept est la différence entre la hauteur vraie de l’étoile mesurée au sextant, et la hauteur calculée de l’étoile. Intercept = hv-hc. L’intercept s’exprime en milles.
Pour ceux qui sont toujours là et qui s’accrochent malgré tout, une petit aparté spirituel avant d’attaquer la suite :
2) Notre programme
Ce programme marche pour l’étoile Dubhé de la constellation de la Grande Ourse, mais il fonctionne également pour n’importe quelle étoile. Il suffit de remplacer les valeurs t (ascension droite de l’étoile le 01/01/16 à 00h00 utc) et u ( déclinaison de l’étoile le 01/01/16 à 00h00 utc). Ce programme marche à partir du 01/01/2016 à 00h00 utc jusqu’à l’année 2100 qui n’est pas bissextile (mais que ce programme intègre comme telle, ce qui est faux).
1) partie 1, transformer la date et l’heure en un seul nombre exploitable (ligne 1/ligne 36).
Jusqu’à la ligne se terminant par , g (ligne 36), le programme va changer l’heure, les minutes, secondes, mois et année de la mesure en un seul nombre décimal qui dans le programme se nomme g. Pour déterminer les années bissextiles on utilise une fonction cosinus (une fonction périodique sinus aurait pu tout aussi bien faire l’affaire); cette fonction sera égale à 1 tout les 4 ans. Quand cette fonction ici appelée i = 1, on peut voir que e (nombre de jours selon les mois) change. La partie avec les « elseif » détermine le nombre de jours écoulés dans les mois depuis le 01/01 de l’année de la mesure jusqu’à l’instant de la mesure.
int(365.25*f) détermine le nombre d’année cumulées entre l’instant de la mesure et le 01/01/2016. int() est une fonction qui ne garde que la partie entière d’un nombre, par exemple int(17.8)=17.
La ligne 35 réduit tout les paramètres de temps à la même unité (le jour), ils sont additionnés pour obtenir g. 2457388.5 (=2451545+5843.5) est le jour julien le 01/01/16 à 00h00.
2) partie 2, déterminer l’angle horaire du point vernal (ligne 37/ligne 45).
Ligne 37, 100+5.5/60 est l’angle horaire du point vernal ahso le 01/01/16 à 00h00 utc.
Aux lignes 37 et 38, grâce à g, on calcule ahso au moment de la mesure en décimal. On sait que le point vernal effectue en 24 heures plus de 360 degrés; pour avoir sa vitesse moyenne précise il suffit de diviser la distance effectuée (360 degrés de révolution entre 2 équinoxes successives en 1 an) par la durée mise par le point vernal. Cette durée correspond à l’année tropique moyenne longue de 365.2421898 jours. Donc (360/(365.2421898)+360)/24=15.0410686… Soit la vitesse moyenne environ du point vernal par heure (pour l’année 2000. Elle diminue très légèrement chaque année).
La durée de l’année tropique moyenne diminue actuellement environ de 5,24 secondes par siècle, -0.0524*16/(24*3600*36525) est donc le calcul de cette diminution de temps entre le 01/01/16 et 2016.
-0.0524*(g-2451545-5843.5)/(24*3600*36525) est le calcul de cette diminution de temps entre 2016 et l’instant de la mesure.
Entre les lignes 38 et 43, le programme donne la valeur de z (ahso) correcte, car avant ce passage z va rapidement être supérieur à 360.
z>DMS transforme les données décimales de z en données sexagésimales (degrés, minutes, secondes).
3) Partie 3, (ligne 46/ligne 76) calcul du relèvement calculé et de l’intercept.
Au début de cette étape on change les données sexagésimales du point estimé et de l’angle mesuré en donnée décimales exploitables pour les calculs. Dans le programme j’aurai aussi pu intégrer la collimation et l’excentricité du sextant employé mais je l’ai pas fait (c’est un mack 3…). Lignes 56 et 57 ce sont respectivement l’ascension droite puis la déclinaison de l’étoile Dubhé le 01/01/16. Ligne 58 à 61 on utilise les équations de la précession pour obtenir les coordonnées céleste de Dubhé à l’instant de la mesure. La ligne 62 calcule l’ascension verse de l’étoile au moment de la mesure, et…Et allez hop pour les irréductibles encore présent, petite pause contemplative ils le méritent bien ! (si ça peut en plus attirer plus de visiteurs sur le blog…)
Alors on en était où… Ha oui ;
Le reste du programme reprend les formules vues au début. La fonction If utilisée entre la ligne 70 et la ligne 72 détermine l’azimut vrai. Et maintenant, utilisation test !
3) Test
Pour faire un point d’étoiles réussi on a besoin de plusieurs ingrédients :
-Un horizon clair et dégagé.
-Une montre bien calée sur l’heure du méridien de Greenwich.
-Une TI89, une calculatrice programmable ou des éphémérides.
-Un sextant ou un truc pour mesurer la hauteur des astres.
-Une carte hauturière.
Pour ma part le jour de la mesure l’horizon n’était pas très net, et j’ai utilisé un vieux sextant mack 3 pour la faire du coup ça manque quand même un peu de précision. En plus la mesure s’est faite sur la Manche, donc la différence de hauteur d’eau due à la marée a pu aussi jouer sur cette précision.
Les conditions m’on permis d’effectuer 3 mesures, une sur Dubhé, une sur l’étoile polaire et une autre sur Alkaid (le bout du manche de la casserole sur la grande ourse). On reste donc malheureusement sur 3 étoiles très proches, mais ça donne déjà une petite idée malgré tout. Le point estimé e (choisit arbitrairement sur la carte) utilisé est de latitude 49°50′ Nord, et de longitude 1°5′ Est. Donc les coordonnées de e sont positives (latitude négative si Sud, longitude négative si Ouest).
Résultats:
.Pour Dubhé, la hauteur vraie est de 35°52′ relevée à 22h 32 min 52 secondes (heure locale, donc en UTC on enlève 2 heures) le 15/08/16. Le programme calcule ce résultat :
relèvement calculé = 325.5° ; intercept = -22.423 miles.
.Pour Polaris, la hauteur vraie est de 48°46′ relevée à 22h 35 min 2 secondes. Du coup on obtient :
relèvement calculé =359.007° ; intercept=-47.113 miles.
.Pour Alkaid, la hauteur vraie est de 44°31′ relevée à 22h 28 min 42 secondes. Donc ça donne :
relèvement calculé= 299.38 ° ; intercept=49.285 miles.
Donc en utilisant la carte, on part du point estimé e, puis pour chaque relevé on trace l’intercept ; du point e vers l’étoile si ce dernier est positif, et du point e vers la direction opposée à l’étoile si l’intercept est négatif. On peut ensuite tracer les droites de hauteur qui sont perpendiculaires aux intercepts afin de définir un triangle de positionnement. Alors le point obtenu nous situe environ à 80 km au sud de Fécamp (ma carte routière était trop petite pour tracer convenablement les droites de hauteur)… Alors que les mesures ont été prises à Pourville près de Dieppe… Il faudrait refaire un point d’étoile avec un horizon plus net et un sextant à tambour peut-être, avec des étoiles bien distancées également.
Ce petit programme fonctionne bien pour corriger les coordonnées célestes des étoiles, pour l’angle horaire du point vernal il est précis à 1° prêt (ça fait une marge d’erreur de 0.3 % environ). Il se base sur une année tropique moyenne or elle change tout les ans selon un nombre important de paramètres tels que la vitesse de la Terre autour du Soleil qui change au périhélie et à l’aphélie avec les lois de Kepler, l’influence de la Lune et des autres planètes également. Autrement dit en réalité la vitesse du point vernal n’est pas complètement uniforme mais varie un peu.
Pour améliorer ce programme on pourrait inclure la collimation, l’excentricité du sextant, également faire en sorte d’avoir directement les coordonnées des points d’intersections des droites de hauteurs à voir…Pourquoi pas améliorer la précision du point vernal et tenir compte de la nutation, Bradley,l’âge du capitaine…