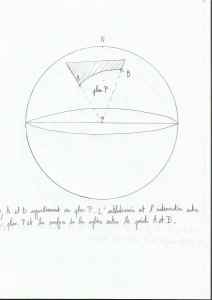
Normalement sur une surface plane le chemin le plus court entre deux points est la droite qui passe part ces deux points, point barre. Sur une sphère comme la terre par exemple, ça se complique un peu; on va alors parler de loxodromie et d’orthodromie (voir la page sur la projection de Mercator). La distance la plus courte sur le globe entre deux positions sera l’orthodromie : c’est la trajectoire confondue avec le demi arc de grand cercle du globe, le demi grand arc est un plan qui coupe le centre de la sphère et les deux positions. Le grand cercle est un cercle capable d’être tracé sur la sphère et dont le périmètre égalise celui de la sphère. Si sur le globe on suit une route nord/sud ou sud/nord(bref si on suit un méridien), ou que l’on suit l’équateur alors on est déjà sur une route orthodromique, du coup pour les calculs qui vont suivre on s’en fout.
Exemple d’une orthodromie:
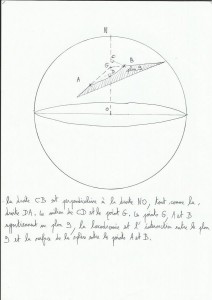
La loxodromie est la droite que l’on trace sur une carte Mercator classique de nav (excepté les routes suivant l’équateur ou un méridien), elle coupe les méridiens avec à chaque fois le même angle. En fait, à cause des caractéristiques de la représentation de Mercator ce n’est pas la route la plus courte; si on traçait correctement la route la plus rapide sur la carte, c’est à dire l’orthodromie, elle ne serait pas représentée par une droite mais par une courbe. Si on est dans l’hémisphère nord elle sera bombée vers le nord, inversement pour l’hémisphère sud (plus l’on se rapprochera des pôles, plus elle sera bombée). En gros l’orthodromie est un problème intéressant pour les longues navigations, plutôt proches des pôles et plutôt orientées est/ouest ou ouest/est. Bref pour une sortie dominicale tranquilou en pédalo c’est pas indispensable de s’en inquiéter quoi.
Exemple d’une loxodromie:
Pour les calculs c’est simple on va utiliser les mêmes trucs que pour trouver la formule de la droite de hauteur : théorème de Pythagore, produits scalaires, trigo et trigo sphérique. La seule notion à utiliser en plus est la loi des sinus (pour trouver le cap de départ de la route orthodromique).
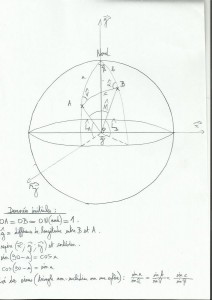1) Calcul de la distance orthodromique (sur le schéma, la distance c, soit l’angle M)
Dans le schéma, on symbolise le globe par une sphère de rayon 1, de centre o inscrite dans un repère cartésien en 3D (x;y;z) d’origine o également. les point A, B et N (pour le nord) sont sur la sphère donc OA=OB=ON=1. Le point A appartient ici au plan (y;z), donc il est de coordonnée o sur l’axe des x. L’angle g est la différence de longitude entre B et A, g ne dépasse pas 90 degrés. L’angle La est la latitude de A et l’angle Lb la latitude de B:
2) Calcul de l’angle V
L’angle V donne le cap initial à emprunter pour suivre l’orthodromie:
En fait, en navigation dès que l’on a une position précise il faut à chaque fois recalculer cet angle pour se repositionner correctement sur l’orthodromie. En pratique ce n’est pas forcément utile de suivre à tout prix cette route, les systèmes météo vont être la priorité en général. Mais chercher à s’en approcher sur une transat par exemple peut permettre d’économiser des milles en optant pour une route composite météo/orthodromie.
PS : dans l’article « programmer une ti89 pour la navigation », il y a un petit programme donné pour calculer la distance orthodromique et l’angle V. Bon il est nul…Avec l’aide d’un bon bouquin (navigation en haute mer de olivier stern-veyrin) j’en ai fait un autre qui compare en plus le gain entre la route orthodromique et loxodromique, et qui calcule le vertex.
Ce programme ci-dessous donne en effet la valeur absolue du vertex en latitude, et sa distance en longitude par rapport au point de départ, seulement sur des routes bien orientées est/ouest. Il donne une valeur approchée de la loxodromie (distance), il existe une formule plus précise (voir wikipépé) mais je n’ai pas réussit à la programmer.
Programme de calcul de l’orthodromie:
J’ai vérifié le bon fonctionnement du programme avec le site « https://www.aero-training.fr/calculer-une-orthodromie.html ». il marche très bien pour la distance orthodromique et le cap orthodromique, comme le cap de la loxodromie. Pour la distance loxodromique il reste précis mais il perd en précision au delà de 400 Mn environ.