A la recherche du salon annuel de la charentaise à Tripaille-en-Paumé, de renommée plutôt locale, vous réalisez avec une stupeur effrayante une erreur sur votre itinéraire. Au lieu d’emprunter la sortie d’autoroute A234 en direction de la zone indus de Létron-la-Trine, vous avez bifurqué trop tôt en prenant le chemin du siège social de l’amicale de sculpture sur boîtes à camembert au carrefour de Bermudaille-en-Paté… Waaah la tuile! Impossible de se situer sur la carte! Bon y a peut-être moyen au moins de définir sa latitude… Sinon on peut aussi allumer le gps ou demander son chemin se sera quand même plus efficace!
1) Le soleil, un bâton, un truc pour mesurer…Et le bon moment
On pense souvent que la découverte de la Terre ronde comme un ballon de foot est attribuée à Christophe Colomb, en fait la réalité est un peu plus complexe. Ce dernier a prouvé cela de façon empirique avec ses voyages, mais il a démontré une théorie déjà évoquée depuis longtemps. Plusieurs siècles plus tôt(5ème siècle avant JC)Platon considérait déjà la Terre comme sphérique. En effet les Grecs avaient déjà noté le caractère courbe de la surface terrestre(un bateau faisant cap sur l’horizon voit d’abord sa coque disparaître, puis le bas de son mât, et enfin le reste). Mais au 2ème siècle avant JC un grec a réussi grâce à une méthode très simple à calculer la circonférence de notre ballon de foot, avec une précision assez incroyable pour l’époque(700 km de différence seulement avec notre valeur actuelle!)c’est Eratosthène.
Son raisonnement était le suivant: comme la terre est courbe, alors les rayons du soleil atteignent la surface terrestre avec des angles différents. Il a ajouté à ça un peu de trigonométrie pour assaisonner et c’est tout.
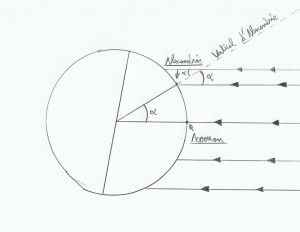
Pour son calcul il considérait les rayons du Soleil parallèles entre eux(car cet astre par rapport à la Terre est bien plus volumineux et surtout très éloigné). A l’époque il savait que lors du 21 juin(solstice d’été), à midi local à Assouan les silhouettes verticales ne dessinaient pas d’ombre, il a donc déduit qu’à ce moment là le Soleil se situait sur la droite perpendiculaire à la tangente passant par Assouan. Après tout ça il est facile de deviner la distance angulaire entre Assouan et Alexandrie(angla alpha sur le schéma), en plantant un bâton à Alexandrie et en observant son ombre à midi local le 21 juin, on trouve alpha.
Il faut planter le bâton le plus droit possible(utiliser un fil à plomb)pour avoir une mesure la plus précise possible(pour être encore plus précis, utiliser de préférence un bâton grand et fin, et un sol bien plane). En connaissant la taille de notre bâton et en mesurant l’ombre on peut rapidement retrouver alpha avec un peu de trigo(l’ensemble forme un triangle rectangle). En effet Tan(alpha)=côté opposé/côté adjacent donc Tan(alpha)=ombre/bâton. Eratosthène a trouvé un angle alpha égal à 7, 2° environ.
Comme il connaissait la distance entre les deux villes, et que 7, 2° équivaut à 1/50ème de 360°(soit la circonférence totale de la Terre)il a alors multiplié la distance entre les deux villes par 50 ce qui donna 39350 km(la valeur réelle approximative est de 40033 km).
Bon vous allez dire c’est bien gentil tout ça mais pour aller à Tripaille-en-Paumé on est pas plus avancé là! Oui c’est sûr, mais en prenant le problème d’une autre façon on peut trouver sa latitude, à peu près en tout cas…
En connaissant la règle des quatre 21(voir article « la sphère céleste »)on sait environ la position du pied de l’astre du Soleil aux solstices(+ou-23°26′) et aux équinoxes(0°)en latitude. Donc si dans ce cas on veut connaître la latitude d’Alexandrie il suffit d’additionner l’angle alpha à la latitude d’Assouan. Assouan a une latitude d’environ 24°(logique puisqu’au solstice d’été, le 21 juin le pied de l’astre Solaire a une latitude de 23°26′, or à cette date il n’y a pas d’ombre pour les silhouettes verticales à Assouan)donc Alexandrie a une latitude de 31° à peu près.
Maintenant dans notre cas si nous sommes perdu le 22 septembre et que nous calculons alpha à midi local(pour trouver le midi local avec le bâton, c’est le moment où ce dernier dessinera sur le sol l’ombre la plus courte dans la journée, car à ce moment là le soleil sera le plus haut sur l’horizon), si alpha est égal à 51° cela veut dire que notre latitude est de 51°(car le jour de l’équinoxe d’automne la latitude du pied de l’astre Soleil=0° à midi local environ). Après pour avoir la position en latitude du pied de l’astre Soleil à l’année il faut trimballer les éphémérides dans la boîte à gants mais bon là…
Remarque: si on arrive à définir l’heure précise du midi local de notre lieu(grâce à l’ombre du bâton qui rétrécit jusqu’à midi local puis qui réaugmente ensuite), et que notre montre est pile réglée à l’heure UT, et que par miracle on a à disposition les éphémérides dans la boîte à gants alors on pourra trouver aussi approximativement notre longitude.
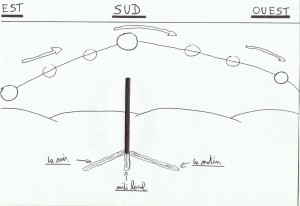
Pour trouver notre midi local avec précision, on va faire un peu la même méthode employée pour la méridienne(voir article « La Méridienne »). Comme le soleil reste à son zénith un certain temps, difficile de trouver le temps exact du midi local en mesurant juste la taille de l’ombre quand elle semble être la plus réduite. En fait on va prendre une mesure de l’ombre quand le soleil est orienté sud-est (en notant l’heure à ce moment là) avec un fil tendu partant de la base du bâton, et on trace au sol un arc de cercle(de rayon égal à cette mesure). Quand l’ombre recoupe notre tracé(le soleil va se rapprocher de l’ouest) on note aussitôt l’heure; l’heure du midi local est alors la somme de ces deux heures divisée par deux.
Dans les éphémérides, on retrouve l’heure de passage du soleil au méridien de Greenwich(le midi local de Greenwich). Donc si notre montre est en heure UT précise, que l’on a réussit à définir notre midi local alors on trouvera notre longitude. Le soleil évolue autour de la Terre(dans notre référentiel bien sûr!)au rythme de 15° par heure environ(cette vitesse est de toute façon indiquée de façon plus précise dans les éphémérides), donc notre longitude=(heure midi local-heure midi local Greenwich)*15.
2) Le pendule du professeur Tournesol
Dans l’article « Coriolis », on a vu que plus l’on s’approchait des pôles et plus Coriolis avait tendance à dévier les corps en mouvement sur de longues distances(vent et courant)vers la droite dans l’hémisphère nord et la gauche dans l’hémisphère sud. Inversement plus l’on s’approche de l’équateur et plus cette « force » s’annule. Donc garé sur le parking de l’église entre Brignolle-la-Farfouillette et Létron-la-Trine, on est en droit de se demander si il n’existe pas un lien ou une formule entre Coriolis et le changement de latitude…Quand on s’ennuie faut bien s’occuper!
On peut effectivement trouver un lien par le biais du pendule de Foucault, son principe fonctionne un peu comme un gyroscope. En gros lorsque l’on fait osciller un pendule(on considère les forces de frottement nulles, le mouvement d’oscillation continue indéfiniment), son plan d’oscillation va rester fixe par rapport à la rotation de la terre sur elle-même, en fait c’est le plan sous le pendule qui va tourner par rapport à lui. Il est facile de déduire la vitesse de rotation du plan du pendule si il est situé pile sur l’un des deux pôles:
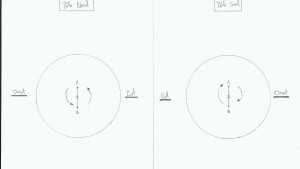
On vas dire que le pendule oscille entre A et B. Si le pendule se situe pile sur le pôle Nord alors le plan sous le pendule va tourner à la vitesse de 15° par heure environ dans le sens anti-horaire(car la terre tourne sur elle-même en 24 heures donc 360°/24 heures, et le soleil se couche à l’Ouest). Au pôle Sud se sera la même vitesse mais dans le sens horaire, et à l’équateur comme Coriolis est nulle le plan sera fixe par rapport au plan d’oscillation du pendule. Mais alors à Brignolle-la-Farfouillette, comment ça se passe? En fait cela crée un mouvement apparent du pendule dans le sens opposé(pôle Nord, le pendule tourne en sens horaire et au pôle sud en sens anti-horaire).
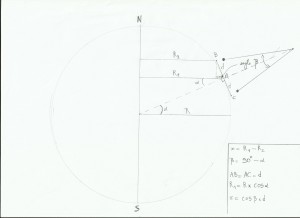
Et puis la vitesse de rotation va dépendre de la latitude du pendule, grâce à la différence de vitesse linéaire selon la latitude. Sur le schéma suivant les points B, A et C sont situés à des latitudes différentes, leur vitesse angulaire terrestre est la même(360° en 24 heures), mais pas leur vitesse linéaire(car la circonférence de la Terre diminue quand la latitude augmente, du coup le point aura moins de chemin à parcourir en 24 heures, donc sa vitesse linéaire sera plus lente si sa latitude augmente. Sur ce schéma le centre du pendule est A et il oscille entre B et C; la latitude de A est l’angle alpha et R le rayon de la Terre:
La vitesse linéaire de A est égale à la vitesse angulaire de la Terre(w) multipliée par R1 donc Va=w*R1; R1=cos(alpha)*R. Du coup Va=w*cos(alpha)*R.
Vb=w*R2, et R2=R1-x. x=cos(bêta)*d d’après la trigo, or l’angle bêta=90°-alpha donc cos(90°-alpha)=sin(alpha). x=sin(alpha)*d. Donc R2=cos(alpha)*R-sin(alpha)*d, Vb=w*(cos(alpha)*R-sin(alpha)*d)
Avec un raisonnement analogue on trouve Vc=w*(cos(alpha)*R+sin(alpha)*d)
Au final on remarque que Vc>Va>Vb, et entre chacune de ces vitesses la différence est de w*sin(alpha)*d. Cette différence entre les vitesses va créer le mouvement apparent du plan sous le pendule. On peut en déduire que la vitesse angulaire de ce plan est de w*sin(alpha), autrement dit la vitesse de rotation angulaire de la Terre multipliée par le sinus de la latitude(on enlève d qui est la largeur du plan, indépendante de la vitesse angulaire). Pour conclure on peut écrire cette équation:
angle de rotation par heure=15*sin(latitude)
(Remarque: aux pôles avec une latitude de 90° on retrouve le principe énoncé au-dessus, tout comme avec une latitude de 0° à l’équateur.)
3) Rappel
La hauteur de l’étoile polaire sur l’horizon donne aussi notre latitude(article « se positionner sans gps ni calculatrice »). Après je n’ai pas encore essayé mais sachant que Mintaka(constellation d’Orion) est quasiment située sur l’équateur céleste, peut-être que sa hauteur sur l’horizon moins 90° donne notre latitude…à voir. Sinon pour retrouver son chemin on peut aussi demander sa position au premier piéton croisé, ça ira plus vite!