La méridienne est facile à mettre en place et ne nécessite pas beaucoup de calculs, par contre la droite de hauteur c’est un peu l’usine à gaz si on loupe une étape. Cependant cette méthode présente un avantage par rapport à la méridienne: on peut déterminer sa position à tout moment de la journée, il suffit de faire deux observations de la hauteur du soleil(au moins deux heures d’écart pour plus de précision). En cas de ciel partiellement couvert, la méthode de la droite de hauteur est une bonne alternative si à midi local le soleil se cache derrière les nuages.
1)Principe
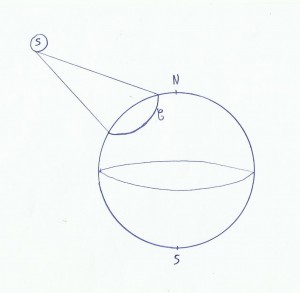
La mesure d’une hauteur du soleil à un moment de la journée nous positionne sur un cercle à la surface du globe:
Ce cercle C, lorsque l’on est dessus nous fait voir le soleil sous une hauteur précise. Cette hauteur appelée hauteur calculée(Hc) se calcule, elle dépend de notre position(que l’on estime, par exemple en prenant comme point estimé le dernier fait dans le livre de bord)et du moment de la journée(le pied de l’astre n’aura pas la même position)où l’on mesure Hv. Ensuite on compare Hc à Hv, la hauteur vraie c’est à dire celle mesurée par le sextant. Si Hv>Hc, alors on reporte le point vers le soleil, sinon c’est l’inverse. La différence entre Hv et Hc est l’intercept.
Pour la droite de hauteur il y a des conditions limites:
20°<Hv<80°
Intercept<30 Miles
-60°<latitude d’observation<60°
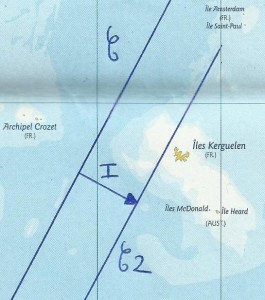
Sur la carte, Le cercle C où l’on voit le soleil sous la hauteur calculée se trace sous forme de droite car sur le globe c’est un grand cercle pouvant être réduit à l’état de droite sur une carte de moindre échelle. Le véritable cercle où l’on est(celui où l’on observe le soleil avec la hauteur Hv)se trouve grâce à l’intercept appelons le C2. C2 se matérialise aussi en droite, c’est la droite de hauteur.
I est l’intercept, en fait on fait un transfert de droite. Si Hv>Hc, on translate la droite C vers le soleil sous la forme de la droite C2, sinon c’est l’inverse. En pratique on ne trace pas C, l’intercept se trace à partir du point estimé sur la carte.
Donc pour une seule observation/mesure de la hauteur du soleil à un moment de la journée, nous pouvons nous positionner sur une droite. Pour avoir une position en latitude/longitude il va falloir faire une deuxième observation. Quand on aura tracé cette deuxième droite de hauteur qui en découle il suffira de translater C2 selon notre route fond entre les deux observations, l’intersection finale nous donnera notre position au moment de la deuxième observation.
2)Le vif du sujet
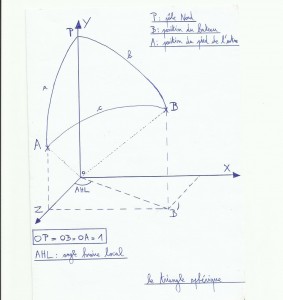
Le calcul de Hc demande un peu de trigonométrie(voir trigo) et un soupçon de produits scalaires, le mieux est de rentrer la formule dans une calculatrice programmable style ti89. Sinon la méthode pour la retrouver est la suivante: on considère le globe terrestre comme une sphère de rayon 1, et incluse dans un repère cartésien où l’origine est le centre de cette sphère(non non, n’allumez pas encore le gps ça va le faire!). B est notre position estimée, A est la position du pied de l’astre calculée au moment de la mesure de Hv, P est le Pôle Nord.
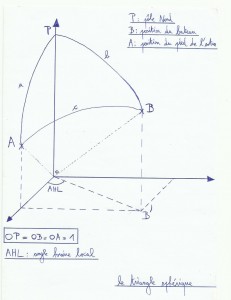
On obtient trois segments sphériques a, b et c. a=90°-D(déclinaison du soleil à l’instant de mesure de Hv), b=90°-Le(latitude de notre point estimé), c=90°-Hc.
AHL=AHG-G(angle horaire du soleil, angle entre le pied de l’astre et Greenwich, moins la longitude de notre point estimé).
Le but du jeu va être de mettre tout ça en équation pour déterminer Hc. Pour cela on va faire un produit scalaire des vecteurs 0A et OB(pfffiouuuuu…..).
On va utiliser notre repère cartésien pour définir ces vecteurs.
0A: Sur l’axe des X, OA=0. Sur l’axe des Y, OA= sin(a) et sur l’axe des Z OA=cos(a).
0B: Sur l’axe des X, OB=sin(b)*sin(AHL), sur l’axe des Y OB=sin(b)*cos(AHL) et sur l’axe des Z OB=cos(b).
Le produit scalaire de deux vecteurs dans un repère cartésien se fait en multipliant leurs coordonnées que l’on additionne, soit OA(X,Y,Z) et OB(X’,Y’,Z’):
XX’+YY’+ZZ’=0+sin(a)*sin(b)*cos(AHL)+cos(a)*cos(b)
On trouve aussi le produit scalaire en multipliant la norme des deux vecteurs par le cosinus de l’angle entre les deux(n’oublions pas que 0A=OB=1):
OA*OB*cos(c)=1*1*cos(c)=cos(c)
Conclusion: cos(c)=sin(a)*sin(b)*cos(AHL)+cos(a)*cos(b), donc:
cos(90°-Hc)=sin(90°-D)*sin(90°-Le)*cos(AHL)+cos(90°-D)*cos(90°-Le), donc:
sin(Hc)=cos(D)*cos(Le)*cos(AHL)+sin(D)*sin(Le)
Voilà pourquoi il vaut mieux noter directement la formule quelques parts…faire ça à la table à carte dans une mer mouvementée, après avoir mangé un cassoulet bien fournit, ça peut devenir un peu difficile!
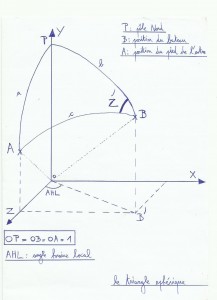
Les ennuis ne sont pas terminés, nous avons Hv, Hc donc nous avons notre intercept. C’est bien gentil, mais comment tracer notre droite C sur la carte? il nous manque une donnée, l’azimut. L’azimut est l’angle entre le vertical du pôle Nord et le vertical de l’astre. On l’appelle Z(en gros c’est le relèvement exact du soleil par rapport à notre lieu d’observation). Pour le trouver on calcule d’abord Z’.
Pour trouver l’angle Z’ on reprend la formule vue un peu auparavant(formule de permutation circulaire): cos(c)=sin(a)*sin(b)*cos(AHL)+cos(a)*cos(b). Ce qui nous intéresse c’est l’angle Z’, donc: cos(a)=sin(b)*sin(c)*cos(Z’)+cos(c)*cos(b)
donc, cos(90-D)=sin(90-Le)*sin(90-Hc)*cos(Z’)+cos(90-Hc)*cos(90-Le), et du coup:
sin(D)=cos(Le)*cos(Hc)*cos(Z’)+sin(Hc)*sin(Le) et au final cos(Z’)=(sin(D)-sin(Le)*sin(Hc))/(cos(Le)*cos(Hc))
Une fois Z’ déterminé, pour trouver Z(le vrai azimut, soit le relèvement calculé du soleil)c’est simple:
Z=Z’ si c’est le matin(si le soleil est à l’Est), et Z=360°-Z’ si c’est l’aprèm(si le soleil est à l’Ouest).
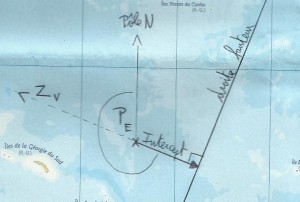
Dès que l’on a l’intercept et l’azimut vrai, on peut alors tracer notre droite de hauteur à partir de notre point estimé de départ. L’azimut qui est le relèvement calculé du soleil nous donne la direction pour tracer l’intercept(intercept sera perpendiculaire à la droite de hauteur), l’intercept nous donne la distance entre la droite de hauteur et le point estimé, et aussi de quel côté on tracera la droite par rapport au point(vers le soleil, en s’éloignant du soleil).
Dans l’exemple, Pe est le point estimé de départ, Zv est l’azimut vrai. Dans ce cas ci Hv<Hc, c’est pourquoi l’intercept est de sens opposé au soleil.
Le mieux pour cette méthode est d’avoir une calculatrice programmable style texas instrument(ti89 c’est bien), pendant un temps l’almanach du marin breton incluait une feuille de programme à rentrer dans la calculette et bien pratique malgré deux ou trois erreurs à corriger. Je crois qu’il existe aussi des calculettes spéciales astro conçues pour ça. Le marin breton explique très bien cette méthode.