Pour les amateurs de bande dessinées, Newton est le personnage de rubrique à brac(Gotlib) qui a le don de se prendre une pomme sur la tête dans n’importe quelle circonstance, et accessoirement il a été un grand scientifique connu pour ses travaux sur l’optique, le calcul différentiel et dans le cas qui nous intéresse les lois de la gravitation. Ces lois expliquent le phénomène des marées.
1ère loi: la quantité de mouvement(Q) est égale au produit de la masse(M) du corps en mouvement et de sa vitesse(V). Q=M*V, en gros plus un objet est lourd et rapide et plus c’est galère pour l’arrêter.
2ème loi: La somme des forces appliquées à un objet en mouvement accéléré est égale à la masse de cet objet multipliée par sont accélération. Si l’objet est au repos(vitesse constante ou immobile)alors d’après la formule la somme des forces appliquées est donc égale à 0.
3ème loi: Une force appliquée à un objet crée une force antagoniste(ex force de gravité/poussée d’Archimède)de même direction et intensité mais de sens opposé.
4ème loi: La force gravitationnelle(Fg) présente entre deux astres est égale à la constante gravitationnelle(Gn)multipliée par les deux masses des astres(M1 et M2) et divisée par la distance qui les sépare au carré(D carré). C’est une loi de carré inverse, l’intensité de la force de gravité décroît très vite quand la distance d’éloignement de l’astre augmente un peu.
Fg=Gn*M1*M2/D carré
1)En gros comment ça marche?
La terre a une surface majoritaire composée d’eau, cette surface se déforme de quelques dizaines de centimètres au large des océans dans la zone intertropicale sous l’influence de la gravité(Soleil et Lune).
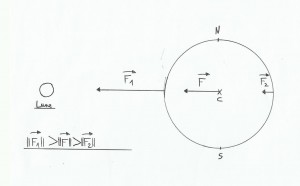
La force de gravité ne se répercute pas de la même manière sur le globe, elle est plus forte à proximité de la Lune. On peut en déduire qu’il y a deux marées hautes aux points d’application des forces F1 et F2(car ici la force de gravité est plus faible, c’est la force centrifuge qui l’emporte). D’après la 4ème loi du début on peut calculer F, F1 et F2.
F=Gn*Mlune/D(terre et lune)au carré
F1=Gn*Mlune/D(terre et lune-rayon terre)au carré
F2=Gn*Mlune/D(terre et lune+rayon terre)au carré
Mlune=7,36*10 puissance 22 kg
D(terre et lune) = 384000000 m
rayon terre = 6350000 m
Gn = 6,67*10 puissance -11 m cubes/kg/secondes
En dégainant sa calculatrice on obtient donc :
F environ égal à 3,3*10 puissance -5 mètres par seconde, F1 3,4*10 puissance -5 mètres par seconde et F2 3,2*10 puissance *-5 mètres par seconde. La force de marée subie à la surface des océans est la différence entre F et F1 et F et F2. Donc cette force équivaut environ à 1*10 puissance -6 mètres par seconde avec la Lune seule. En s’amusant à faire pareil avec les données du Soleil(poids et distance terre/soleil)on trouve environ 0,5*10 puissance -6 mètres par seconde(on voit bien la loi du carré inverse de la distance, bien que le soleil soit énorme, sa grande distance de la terre réduit considérablement sont influence. Par contre si la planète Mercure avait de l’eau, ça ferait une sacrée marée perceptible!).
La lune subit de la part de la terre aussi une force de marée bien plus importante(F3), c’est pourquoi elle nous montre toujours sa même face; au cours des siècles cette force a rendu la période de rotation de la lune égale à sa période de révolution autour de la terre, bref c’est un peu le bordel…
rayon lune = 1750000 mètres
masse de la terre = 5,97*10 puissance 24 kg
F3 = Gn*Mterre/D(terre et lune-rayon lune) au carré
F4(centre lune) = Gn*Mterre/D(terre et lune) au carré
la force de marée sur la lune est donc = 3*10 puissance -5 mètres par seconde, 30 fois plus importante que celle exercée par la lune sur terre!
2)Pourquoi à la côte les quelques dizaines de centimètres de différence du large se tranforment en mètres (la vache il est long ce titre!)
Parce que la profondeur diminue pour résumer