To make a program usefull for our position and working with the Sun., equation of time has been used, thus difference between solar average time and solar true time. This equation includes the true speed taken at "t" time of earth around the sun, irregular speed in time because of its elliptic way (see Kepler's laws). Now let's see how this equation was found, method found should maybe help us later in case of planet path calculations usefull for navigation too (Mercury, Venus, Mars, Jupiter, Saturn), knowing that to write a position program with planets we will have to change of referentiel (from a heliocentric to a geocentric referentiel, something about). To write this article i have used a lot "the theoretical minimum" written by L. Susskind (not always easy to understand quickly but really interesting, I used his book on classical mechanics) and also physics courses available on youtube of Richard Taillet (mechanical, semester 2, course 3), very clear and well explained where from motion equations he proves elliptic path and Kepler's laws for 2 systems. Well I hope I have not let too much bullshits in the summary of all these steps.
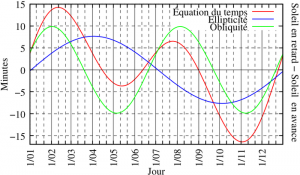
(With this diagram just above, we can see all along a year the shift between the average sun where the earth spin theoreticaly around drawing perfect circles, and the true sun's path)
1) classical mechanics stuff
A system can be resumed in mechanic as a sum up of kinetic energies (Ec) and potential energies (Ep) assigned to it, it's all the system energy (And). kinetic energy could be seen as a kind of "motion energy" of the system, and potential energy, as noticed by its name, energy that could be released by the system (i hope this def is not so bad). For example if we put a ball at the top of a building, ready to be dropped, then at that time its potential energy will be at its peak, and its kinetic energy will be at its weakest level (because the ball is motionless relative to the referential building). Now if you grab this ball just before its crush on the floor, its kinetic energy will be at its maximum (the ball reaches its maximum speed) but this time its potential energy will be almost minimum (it will be at minimum when the ball will hit the ground).
therefore in physics total energy is written like this :
Et = Ec + Ep = 1/2 mv ^ 2 + V(x), with V(x)= Potential of the system. I rated it V(x) because the potential depends on the position of the object studied in a given referential (with our exemple of the ball on the building, the more our building will be high and the more our potential ball will be strong it's nearly that).
with all those things it's possible to find motion equations of an object. but before going a little further it's interesting to define other things (but not too much it could be bothering ).
- a) The potential energy
For central force systems (like planets which undergo a star or an another planet gravity, which can be similar to a point) it's possible to define that the sum up of forces working on the object are equals to negative potential energy gradient : ΣF = -grad(V), there is a negative symbol before grad because the object is attracted towards the point (so acceleration written with a vector will aim at the point if we would draw a diagram of it). We can also define force as follows :
Fi(x)=-∂V(x)/∂xi ; This thing means that the force expressed on a spatial way of the system (here xi) is equal to potential partial derivative compared to this spatial way... I guess. We could also say that a force it's space divergence of a potential energy (in mikado backflip the most of time but well let's go a little further).
According to Newton's laws the sum of the forces is equal to the product of mass and the acceleration of the object. so ΣF = ma. That explains why when the acceleration of an object is zero (motionless object or with a constant speed), then the sum of the forces applied to it equals 0. A force is just an accelerated mass.
- b) derivatives, integrals, partial derivatives
derivatives, partial derivatives
For potential energy we have seen gradient, but what is it ? It's just the sum of space partial derivatives of V potential ; so it's :
Grad (V(x))= ∂(Vx)/∂x+∂(Vy)/∂y+∂(Vz)/∂z
a derivative function in regards to time shows its time rate (we will then talk about velocity, it's the object speed compared to a way choosen in a choosen referential, Cartesian for exemple) but it can also be done in space if the derivative function is derivated regards to space. In fact we could easily derivate a function with any of its parameters (for functions with several variables), not always just time parameter.
The second derivative of a function indicates the rate of change of the first derivative. If the first derivative is velocity, then the second derivative will be object acceleration according to a way choosen in our landmark .
Usually derivatives allows you to notice how will evolve your function (increasing, decreasing, stationary…) and second derivatives are useful when you need to find maximums and minimums in a local range of a function, and other things like making coffe or learning how to understand women.
The derivatives are not exclusively reserved for functions with one variable, they can also be used for functions depending on several variables ; we will then talk about partial derivatives. The idea is almost the same except that when we derivate a function regards to one of its parameters, we consider the other parameters like numbers or simple coefficients. For example, considering the function F(x ;y)= 3x + 2y. If we do ∂F(x ;y)/∂x it gives = 3, and if we do ∂F(x ;y)/∂y = 2 is obtained.
integrals
It's a bit the opposite approach of a derivative, if we could say it like that. if we should define with accuracy this thing we could say that it's an amount of areas under a function. we could deduce that potential is equal to negative integral's force with constant : V = -∫Fdx+constant. nevertheless here we will give up constant (see the principle of gauge invariance for the curious). So it gives V = -∫Fdx.
- c) Lagrangian
in physics, Lagrangian is usefull to find how a system will change with time and space, deduce motion equations, and identify potential symmetries, Its a bit like a swiss knife in fact...Usefull to find action's system too (see the principle of least action for the curious).
Lagrangian : it's just kinetic energy without potential energy of an object studied (at least for our planets, but this is not always the case for all systems), So it gives : L=1/2 mv^2-V(x). The Lagrangian can be considered as a function working with 2 variables, a space variable (induced by the potential energy) and a velocity variable (induced by the kinetic energy). It gives at the end L=L(xi ; dxi/dt). (Dx / dt = velocity on x axis and xi means axes, y and z).
symmetry : In physics it's when we have a lagrangian invariance when the system is moving in one freedom degree (Here we talk about space configuration with degrees of liberty in space, x, y and z). For example, angular moment is a rotation symmetry. so we get dL / dt = 0 in a Lagrangian symmetry linked with time.
- d) Euler-Lagrange
This way allows us, with the Lagrangian's help, to find the combined moment of a system (it will help us to detect the system symmetries) and motion equations.
combinated moment : it's lagrangian's derivative regards to velocity.
Euler-Lagrange equations : it's just : (d/dt)( dL/dVx) – (dL/dx)=0 (for a single freedom's degree, here x. Vx is x's derivative with time, so it's velocity).
2) Find motion's equations of a system around the sun.
- a) The Lagrangian in polar coordinates
We will first try to define the Lagrangian of the system in an orthonormal system (x, y, z), then we will change it to work in a polar way(r and ө, r = radius, in fact distance between 2 systems and ө = angle).
The kinetic energy : it's simple, It's Ec=1/2 m(dx/dt)^2+1/2 m(dy / dt)^2. It is considered that the object moves in a single plan (x, y) thus we get rid of z. If we would have taken care of z we would have spoken of cylindrical polar coordinates.
The potential energy : we will do a little magic trick ; we almost all know that the gravitational force between 2 bodies defined by Newton equals GMm/r^2 (proportional to the product of the masses and inversely proportional to the square of their distance between them). Or we have seen that V = -∫fdx ; so if we integrate GMm/r^2 we will finally get V(r)=-GMm/r (because the potential depends on the distance r which is a variable parameter, G, M and m are considered as constants, remember the example of the skyscraper and the ball).
We know that the Lagrangian is the difference between kinetic energy and potential energy, so :
L = Ec-Ep = 1/2 m(dx/dt)^2+1/2 m(dy / dt)^2+GMm/r
Now we will convert our Lagrangian in polar coordinates. It's more convenient when you want to study a rotating object around an another one. There will be 2 degrees of freedom : r which is the distance between the 2 stars and ө which is in degrees the angle between the pericentre and the position of the rotating object relative to the focal (the sun).
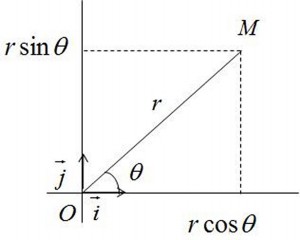
According to the small diagram so we can convert the Cartesian coordinates into polar coordinates as follows :
X=rcos(ө)
Y = rsin(ө)
Then we will just have to substitute in our Lagrangian those new things ; However, in the Lagrangian we talk about velocity but here we have positions only. Before touching our Lagrangian it must will be unavoidable to calculate the first derivatives of X and Y. Taking into account that they are functions products (r with cos(ө) and r with sin(ө)), and ө be regarded as a dependent function of time (so cos(ө) and sin(ө) should also be considered as composite functions in our calculation of derivatives), we will find that :
X’=r’cos(ө)-sin(ө)ө’r (the 'means time derivative, useful to write faster. For example r 'is the time derivative of r).
Y '= r'sin(ө)+ө'cos(ө)r
If we take our derivatives and we stock them in the Lagrangian instead of our first coordinates , we get :
L=1/2 m(r’^2+ө’^2r^2)+GMm/r, in fact our Lagrangian in polar coordinates.
- b) Motion equations
This time we will grab in our toolbox Euler-Lagrange equations. We will use it for our 2 degrees of freedom and it will give us :
(d/dt)( dL/dr’)- (dL/dr)=0 and (d/dt)(dL / dө ')-(dL / dө)=0
When it's solved, we get 2 equations :
r''=rө’^2-GM/r^2 (r '' is the second time derivative of r, acceleration then).
(d/dt) (mө’r^2)=0 (this equation displays a symmetry 's system, thus a Lagrangian stability regards to angular velocity with time. In fact it shows kinetic moment stability of the system when it's spinning around the sun). We could also write this second equation in this form : mө'r ^ 2 = constant.
As we know that m is a mass considered constant, So then we could be more accurate and say r^2ө'= constant = C.
- c) Getting a function of r kind(ө)
This function will allow us to determine the trajectory of a systaem by its polar coordinates. For that, we need the Lagrangian found just before :
L= 1/2 m (r’^2+ө’^2r^2) + GMm/r
We have also established that C=r^2ө’. This constant is simply the area constant, one of the three rules of Kepler's laws. Okay so now we will integrate this constant in Lagrangian's equation and it looks like this :
1/2 r’^2+(1/2) (C^2/r^2)= GM / r + constant (we note that if we simplify writting m disappered, so the mass of the moving object. So we can deduce that the mass of the object does not affect its movement around the main object).
Now we will try to transform our Lagrangian as a function r(ө).
It will then be necessary to determine r as a function depending on the parameter ө, knowing that ө depends on time t ; we will write mathematically :
r'=dr/dt=(dr/dө) (dө/dt) ; r 'is defined here as a composite function.
So in fact it also gives dr(ө(t))/dt=(dr/dө)( dө/dt), so at the end ө’(dr/dө).
From this writting we change writting of the function found before and we get :
1/2 ө '^ 2 (dr/dө)^2 + 1/2 (C^2/r^2)- GM / r = constant
Do not forget that C=r^2 ө’ and so ө’=C^2/r^4 , So from this we change it again and it will serve us this thing :
(C^2/r^4) (dr/dө)^2 + C ^ 2 / R ^ 2 -2GM / r = constant
To simplify our future calculations,we will introduce an intermediate variable : u=1/r or r=1/u.
If we derivate r on ө, resuming r=1/u we get dr/dө=(-1/u ^ 2)( du / dө)
Well let's go one more time for equation modifications from those new things, by inserting it in the pack it gives :
C^2 u^4 (1/u ^ 4) (du / dө)^2 + C^2 u^2 – 2GMu= constante
we simplify : C^2 (du / dө)^2 + C^2 u^2 – 2GMu= constante
We simplify again : (du / dө)^2 + u^2 – 2GMu/C^2=constante
Now we derivate everything with u, then we derivate by ө :
2 (d^2 u/dө^2) (du / dө) + 2u (du / dө) – (2GM/C^2) (du / dө)=0
One notices that the equation could be simplified, and it gives us :
(d^2 u/dө^2) + u=GM/C^2 , it will allow us to calculate u according ө therefore r according ө.
now we have to resolve a differential thing...Not won yet this story. If u is constant we have a solution GM/C^2, but it's still a special solution (it's just if the system's way draw a cercle in space, not an ellipse shape). The solution will be harmonic oscillator like this Acos(ө) + Bsin(ө), equal also Xcos(ө+ө0) with X the motion range. we find also the harmonic oscillator when we study pendulum motions or electricity for exemple. In fact we can deduce that :
u(ө) = GM/C^2 + Xcos(ө+ө0) ; and now it's nice , but we are seeking r(ө) in fact ! well yes then as r = 1 / u, then that's good :
u(ө)=GM/C^2 (1+ (AC^2/GM) cos (ө+ө0)) , – AC^2/GM it's the ellipse eccentricity which is written e.
So : r(ө)= (C^2/GM)/(1-e cos(ө+ө0)). The ө0 is pointless(it is useful if you want to shift function's period that's all) So we get our desired equation :
r(ө)=(C^2/GM)/(1- e cos(ө))
If e is equal to or greater than 0 but strictly under 1, then we have an ellipse trajectory; if e = 1 then our path will be parabolic, and finally if e>1 so we'll have a hyperbole. This equation allows us to guess trajectory regards to rotation's angle, but how to draw this trajectory with time ? In fact we will build the link first with a geometric method, and then by approximation using number sequences.
Small break about the harmonic oscillator : from the harmonic oscillator, solution of the differential equation seen before, we could express the trajectory's equation in an another way. Why ? because , this oscillator solves the following differential equation :
x’’+ Wo^2x=0 , as we can notice it looks like very similar compared to what we have found before : (d^2 u/dө^2) + u=GM/C^2.
In fact oscillator's equation describes a physical system following time without amortization, friction, on the neighborhood of a balanced and stabled position. Wo is a parameter called the natural frequency, it is equal to Wo=2π/To, To is the natural period of the phenomenon.
As we have seen the solution can be written x(t)=Acos(Wot) and y(t)= Bsin(Wot) (they are parametric coordinates), in fact A=xo (x position at time t = 0) and B=Vo/Wo (initial velocity divided by the pulsation). Why ? because when we put t = 0 then x(0)=A (because cos(0)=1 and sin(0)=0) and when we derivate y(t) and x(t) with time, we find y'(t)=WoBcos(Wot), and if we do y'(o) we get y'(o)=WoB so B=y'(o)/Wo (Y'(o)=Vo).
(seeking on google “harmonic oscillator without damping planets”, we drop on this pdf very well explained just above)
3) The elliptical path
P=C^2/(GM), this is called the ellipse parameter, so r=P/(1- e cos(ө)).
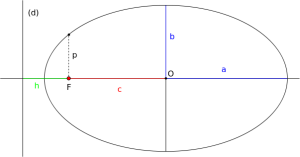
To calculate r max, the distance to aphelion just write ө = 0, we get r max=P/(1-e), and the distance to perihelion just write ө = 180 which gives us r min=P/(1+e). Then to get the diameter's half part of our ellipse we just have to use (r min + r max)/2 which is equal to a= P/(1-e)^2. So if ө = 90 °, that is to say if cos (ө)=0, then P=a (1- e)^2. To set geometrically all the parameters of the ellipse I introduced a small diagram to be clearer :
C = ae and b=a√(1-e^2). F is the focus of the Sun (the stationary sun serving as the origin), e the eccentricity and a the semi-major axis of the ellipse. C is the distance from the focus to the center o of the ellipse.
4) The equation of time
it allows us to get the real sun's velocity around the earth (when we use earth like our referential). According to Wikipedia it is made with center's equation and earth obliquity's equation. there is on wikipépé an another simplified version where we have built something around by using trigo functions, but we will rather stay focused on the first one, egg, ham, and cheese.
- a) Center's equation
Here it is written in the form of a C function working with average anomaly M, thus C(M). The average anomaly is easy to define, it is the average angular velocity of a system or a planet which is mooving (we could also consider that it could be the system's speed if its trajectory was perfectly circular., in fact it's the way reached by the system in one rotation divided by time employed to run this rotation, that's all). So M is to be considered also as a dependent function of time t this time (So we can consider the function C as a composed function because C works with M and M works with t, in fact C depends on t).
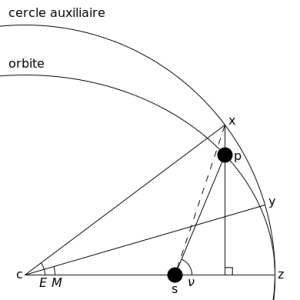
There is Kepler's equation which is able to link average anomaly and excentric anomaly : E-e sin(E)=M, with M average anomaly and E excentric anomaly. However this equation doesn't include true anomaly v. The true anomaly depends on time, but on the diagram there is no geometric bridge between average anomaly and the others. However the previous equation links it to excentric anomaly, but problem : if we know average anomaly (thus time ...) we can not solve the Kepler's equation analytically, So we'll have to approximate a result, find an approximate solution to determine a position of the star regards to time (well ...).
to do this approximate work we will use series, and according to the eccentricity of the path we will employ :
. For an eccentricity's trajectory with e>e0 = 0.6627 ... Thus we will use a Fourier's serie (here, this is the case for objects with high eccentricities like comets).
. For an eccentricity's trajectory with e<e0 = 0.6627 ... Thus we will use a whole serie (For planets useful to navigate it will be whole series, like Earth).
- b) Earth obliquity's equation
This is a function that depends on the ecliptic longitude LE so we can write it R(LE). It allows transferring the ecliptic coordinates into equatorial coordinates of the Sun, more helpful to use. Calculate LE is easy, it is simply the average angular velocity of the Sun around the Earth (geocentric reference) plus C(M) all this is able to correct this speed with trajectory's shape. R(LE) use a formula to make a link between ecliptic and equatorial coordinates (see diagram below).
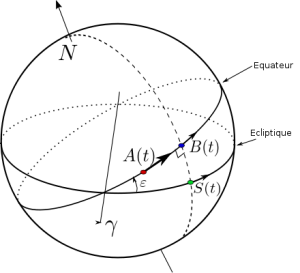
In the diagram just above, Υ represents the vernal point (crossing the equator and the ecliptic to the ascending knot) ; ε is the slope angle between equator and ecliptic which is changing slowly during a long period. A(t) is any point dependent on time t, and motionless on an earth surface so it browses steadily in one sideral day . Point S(t) is aligned between the center of the Earth and the Sun., and makes one revolution per sidereal year, so it has an irregular rate over one year (because of its elliptical trajectory). And B(t) is the intercept between the S meridian(t) and the equator. We get then on earth surface a rectangular and spherical triangle in B(t), giving cos(ϵ)=ϒB(t)/ϒS(t), so YB(t)= Cos(ϵ) ϒS(t). So far so good after it gets complicated somewhat. Then to sum up all this, A(t) spins steadily, S(t) not so B(t) too, then in fact A(t) is connected to the average anomaly and B(t) is connected to the true anomaly ... It can be deduced that the angle between A(t) and B(t) is the true solar hour. Then Hv(t)=angle BA= angle Bϒ+angleϒA.
To define the average solar hour, we'll take the point A(t) because it moves steadily, and we will take an imaginary point derived from S(t) we will call it Sv(t) ; but this one we will imagine that it moves regularly. It gives : Hm(t)=angleSvϒ+angleϒA. As the equation of time is the difference between the average solar hour and the true solar hour, then E(t)=Hm(t)-Hv(t)=angleBϒ-angleSvϒ.
But we know that YB(t)= Cos(ϵ) ϒS(t), or ϒB(t)=tan(YB) and ΥS(t)=tan(ϒS), so :
Tan(angleΥSv + E)= Cos(ϵ) tan(angleΥS)
E(t)=-angleϒSv+arctan(cos(ϵ)tan(angleΥS))
Using a serie and putting y = tan(ϵ/2) for ϵ/2≈0,20, it gives :
R= arctan (cos (ϵ) tan(ϒs))-ϒs
R= arctan (cos(ϵ) tan (λs-π))-(λs-π)
R= -arctan ((sin(2λs) y ^ 2)/(1+y ^ 2cos(2λs)))
R = -y ^ 2 sin (2λs) + ½ y^ 4sin(4λs)-1/3 y ^ 6 sin (6λs)+….
Well, with all that we can do a little positioning program with the Sun., and perhaps also with planets useful for sailing, with the difficulty of referential change to add. For the moon it's more complicated because it undergoes a lot of forces and follows more intricated motions (three pieces problem), larger in a shorter time.